Finite Element Method (FEM) using MATLAB
The Finite Element Method (FEM) is a numerical technique for solving complex differential equations and engineering problems. MATLAB provides a robust environment for FEM analysis, especially in mechanics. This section introduces FEM concepts, examples, and their solutions using MATLAB.
Overview of Finite Element Method
FEM divides a large, complex domain into smaller, simpler parts called elements. The solution to these simpler problems is combined to approximate the solution for the original domain. Example of meshed plate and hollow cylinder can be seen below:

Steps in FEM using MATLAB
The general steps in implementing FEM in MATLAB are:
- Define the geometry and mesh.
- Specify material properties.
- Assemble the global stiffness matrix and force vector.
- Apply boundary conditions.
- Solve the system of equations.
Example 1: 1D Bar under Axial Load
Consider a bar subjected to axial load. The governing equation is:
d/dx(EA du/dx) = F(x)
\[ \frac{d}{dx} \left( EA \frac{du}{dx} \right) = F(x) \]
where E is the modulus of elasticity, A is the cross-sectional area, and F(x) is the distributed load.
% Parameters
E = 2e11; % Modulus of elasticity (Pa)
A = 0.01; % Cross-sectional area (m²)
L = 1; % Length of the bar (m)
n = 4; % Number of elements
F = 1000; % Distributed force (N)
% Element stiffness matrix
k = (E * A) / (L / n);
% Global stiffness matrix
K = zeros(n+1);
for i = 1:n
K(i, i) = K(i, i) + k;
K(i, i+1) = K(i, i+1) - k;
K(i+1, i) = K(i+1, i) - k;
K(i+1, i+1) = K(i+1, i+1) + k;
end
% Force vector
F_vec = zeros(n+1, 1);
F_vec(end) = F;
% Apply boundary conditions
K(1, :) = [];
K(:, 1) = [];
F_vec(1) = [];
% Solve for displacements
u = K \ F_vec;
disp('Nodal Displacements:');
disp(u);
Output:
Nodal Displacements:
1.2500e-08
2.5000e-08
3.7500e-08
5.0000e-08
Example 2: 1D Cantilever Beam with Point Load at the End
A cantilever beam of length L is fixed at one end and subjected to a point load P at the other end. The governing equation for beam deflection is given by the Euler-Bernoulli beam equation:
d4w(x)/dx4 = P / (EI) * δ(x - L)
\[ \frac{d^4 w(x)}{dx^4} = \frac{P}{EI} \delta(x – L) \]
Where:
w(x): Deflection at distancexP: Applied point loadE: Modulus of ElasticityI: Moment of Inertiaδ(x - L): Dirac delta function representing the point load
Parameters
L = 10 m
P = 1000 N
E = 2 × 1011 Pa
I = 8.333 × 10-6 m4
Number of elements: n = 4
MATLAB Code
clc; clear all; close all
% Parameters
E = 2e11; % Modulus of Elasticity (Pa)
I = 8.333e-6; % Moment of Inertia (m^4)
L = 10; % Length of the beam (m)
P = 1000; % Point load (N)
n = 4; % Number of elements
% Element length
Le = L / n;
% Stiffness matrix for a beam element (local)
k_local = (E * I / Le^3) * ...
[12 6*Le -12 6*Le;
6*Le 4*Le^2 -6*Le 2*Le^2;
-12 -6*Le 12 -6*Le;
6*Le 2*Le^2 -6*Le 4*Le^2];
% Assemble global stiffness matrix
K = zeros(2*n + 2, 2*n + 2); % Global stiffness matrix
for i = 1:n
% Global DOFs for element
idx = 2*i-1 : 2*i+2;
K(idx, idx) = K(idx, idx) + k_local;
end
% Force vector
F = zeros(2*n + 2, 1);
F(end-1) = P; % Apply point load at the last node
% Apply boundary conditions (cantilever beam)
K(1:2, :) = []; % Remove rows corresponding to fixed DOFs
K(:, 1:2) = []; % Remove columns corresponding to fixed DOFs
F(1:2) = []; % Adjust force vector
% Solve for displacements
U = K \ F;
% Add back fixed DOFs (displacements and rotations are zero at the fixed end)
U = [0; 0; U];
% Post-processing: Calculate nodal deflections
disp('Nodal Displacements (Deflections):');
disp(U(1:2:end)); % Deflections at each node
disp('Nodal Rotations:');
disp(U(2:2:end)); % Rotations at each node
% Visualization: Plot the deflected shape of the beam
% Nodal positions (x-coordinates of nodes along the beam)
x_nodes = linspace(0, L, n+1);
% Nodal displacements (deflections)
y_deflections = U(1:2:end);
% Apply a scaling factor to amplify deflections for better visualization
scaling_factor = 10; % Adjust the scale for better visibility (change this value as needed)
y_deflections_scaled = y_deflections * scaling_factor;
% Plotting the beam deflection
figure;
hold on;
h1 = plot(x_nodes, y_deflections_scaled, '-o', 'LineWidth', 2, 'MarkerSize', 8); % Deflected shape
xlabel('Position along the beam (m)');
ylabel('Scaled Deflection (m)');
title('Deflected Shape of the Beam under Point Load');
grid on;
axis([0 L min(y_deflections_scaled)-0.2 max(y_deflections_scaled)]); % Set axis limits
% Optionally, you can also add the undeformed shape as a reference:
h2 = plot(x_nodes, zeros(size(x_nodes)), '--k', 'LineWidth', 1); % Un-deformed shape
% Correctly add the legend
legend([h1, h2], {'Deflected Shape', 'Undeformed Shape'}, 'Location', 'best');
hold off;

The output includes the deflection and rotation of each node along the cantilever beam:
Nodal Displacements (Deflections):
0
0.0172
0.0625
0.1266
0.2000
Nodal Rotations:
0
0.0131
0.0225
0.0281
0.0300
Explanation
1. Stiffness Matrix Assembly:
The local stiffness matrix is assembled element-wise into the global stiffness matrix.
2. Boundary Conditions:
For a cantilever beam, the displacement and rotation at the fixed end are zero. These constraints are enforced by modifying the stiffness matrix and force vector.
3. Solution:
The system of equations K * U = F is solved to compute the displacements U.
Example 3: Stress and Strain in 3D Beam with Uniformly Distributed Load (UDL)
A 3D beam with a uniform distributed load (UDL) along its length is analyzed for stress and strain using the Finite Element Method (FEM). The beam is fixed at one end and free at the other. The governing equations involve calculating displacements, stress, and strain.
Parameters
Beam Length (L) = 5 m
Cross-sectional Area (A) = 0.01 m2
Modulus of Elasticity (E) = 200 GPa = 2 × 1011 Pa
Moment of Inertia (I) = 8.333 × 10-6 m4
Uniform Distributed Load (q) = 5000 N/m
Number of elements (n) = 4
MATLAB Code
clear all; close all; clc;
% Parameters
L = 5; % Beam length (m)
A = 0.01; % Cross-sectional area (m^2)
E = 2e11; % Modulus of elasticity (Pa)
I = 8.333e-6; % Moment of inertia (m^4)
q = 5000; % Uniform distributed load (N/m)
n = 4; % Number of elements
% Element length
Le = L / n;
% Local stiffness matrix for a 3D beam element
k_local = (E * I / Le^3) * ...
[12 6*Le -12 6*Le;
6*Le 4*Le^2 -6*Le 2*Le^2;
-12 -6*Le 12 -6*Le;
6*Le 2*Le^2 -6*Le 4*Le^2];
% Assemble global stiffness matrix
K = zeros(2*n + 2, 2*n + 2); % Global stiffness matrix
for i = 1:n
% Global DOFs for element
idx = 2*i-1 : 2*i+2;
K(idx, idx) = K(idx, idx) + k_local;
end
% Force vector for UDL
F = zeros(2*n + 2, 1);
for i = 1:n
% UDL contribution to local force vector
f_local = q * Le / 2 * [1; Le/6; 1; -Le/6];
idx = 2*i-1 : 2*i+2;
F(idx) = F(idx) + f_local;
end
% Apply boundary conditions (fixed end)
K(1:2, :) = []; % Remove rows corresponding to fixed DOFs
K(:, 1:2) = []; % Remove columns corresponding to fixed DOFs
F(1:2) = []; % Adjust force vector
% Solve for displacements
U = K \ F;
% Add back fixed DOFs (displacements and rotations are zero at the fixed end)
U = [0; 0; U];
% Post-processing: Calculate stress and strain
strains = []; % Strain in each element
stresses = []; % Stress in each element
for i = 1:n
idx = 2*i-1 : 2*i+2;
Ue = U(idx); % Element displacements
strain = (Ue(3) - Ue(1)) / Le; % Axial strain
stress = E * strain; % Axial stress
strains = [strains; strain];
stresses = [stresses; stress];
end
% Display results
disp('Nodal Displacements:');
disp(U(1:2:end));
disp('Element Strains:');
disp(strains);
disp('Element Stresses:');
disp(stresses);
% Visualization: Plot the deflected shape of the beam
% Nodal positions (x-coordinates of nodes along the beam)
x_nodes = linspace(0, L, n+1);
% Nodal displacements (deflections)
y_deflections = U(1:2:end);
% Apply a scaling factor to amplify deflections for better visualization
scaling_factor = 100; % Adjust the scale for better visibility (change this value as needed)
y_deflections_scaled = y_deflections * scaling_factor;
% Plotting the beam deflection
figure;
hold on;
h1 = plot(x_nodes, y_deflections_scaled, '-o', 'LineWidth', 2, 'MarkerSize', 8); % Deflected shape
xlabel('Position along the beam (m)');
ylabel('Scaled Deflection (m)');
title('Deflected Shape of the Beam under Uniform Distributed Load');
grid on;
axis([0 L min(y_deflections_scaled) max(y_deflections_scaled)]); % Set axis limits
% Optionally, you can also add the undeformed shape as a reference:
h2 = plot(x_nodes, zeros(size(x_nodes)), '--k', 'LineWidth', 1); % Un-deformed shape
% Correctly add the legend
legend([h1, h2], {'Deflected Shape', 'Undeformed Shape'}, 'Location', 'best');
hold off;

Output
The output includes nodal displacements, strains, and stresses for each element:
Nodal Displacements:
0
0.0247
0.0830
0.1566
0.2344
Element Strains:
0.0198
0.0466
0.0588
0.0623
Element Stresses:
1.0e+10 *
0.3955
0.9327
1.1768
1.2452
Explanation
1. Stiffness Matrix Assembly:
The global stiffness matrix is assembled element-wise using the local stiffness matrix.
2. UDL Contribution:
The uniform distributed load is converted into equivalent nodal forces for each element.
3. Boundary Conditions:
Fixed-end constraints are applied to the global stiffness matrix and force vector.
4. Post-Processing:
Strains are calculated as the change in displacement over the length of each element. Stresses are computed using Hooke’s Law.
Example 4: Heat Transfer in Composite Materials using FEM
Heat transfer analysis in composite materials is crucial for engineering applications. This example considers a composite slab made of two different materials subjected to steady-state heat transfer.
Problem Description
The composite slab consists of:
– Material 1: Thickness = 0.01 m, Thermal Conductivity = 200 W/m·K
– Material 2: Thickness = 0.02 m, Thermal Conductivity = 50 W/m·K
Boundary Conditions:
– Left surface temperature: TL = 100°C
– Right surface temperature: TR = 25°C
FEM Approach
The composite slab is divided into 3 nodes and 2 elements:
– Node 1 at the left surface
– Node 2 at the interface between the materials
– Node 3 at the right surface
MATLAB Code
% Parameters
k1 = 200; % Thermal conductivity of material 1 (W/m·K)
k2 = 50; % Thermal conductivity of material 2 (W/m·K)
L1 = 0.01; % Thickness of material 1 (m)
L2 = 0.02; % Thickness of material 2 (m)
TL = 100; % Temperature at the left surface (°C)
TR = 25; % Temperature at the right surface (°C)
% Conductance of each layer
G1 = k1 / L1; % Conductance of material 1
G2 = k2 / L2; % Conductance of material 2
% Global stiffness matrix assembly
K = [1 0 0;
-G1 (G1+G2) -G2;
0 -G2 G2];
% Global force vector
F = [TL; 0; G2 * TR]; % Enforce T1 = TL
% Solve for nodal temperatures
T = K \ F;
% Display results
disp('Nodal Temperatures (°C):');
disp(T);
% Visualization of Temperature Distribution
% Create a plot of temperature across the material thickness
x = [0, L1, L1+L2]; % Positions: 0 (left), L1 (end of material 1), L1+L2 (end of material 2)
temperature = [T(1), T(2), T(3)]; % Temperatures at the corresponding positions
% Plotting the temperature profile
figure;
plot(x, temperature, 'o-', 'LineWidth', 2, 'MarkerSize', 8);
xlabel('Position (m)', 'FontSize', 12);
ylabel('Temperature (°C)', 'FontSize', 12);
title('Temperature Distribution Across Two Material Layers', 'FontSize', 14);
grid on;
% Add shaded regions for the materials
hold on;
fill([0, L1, L1, 0], [min(temperature)-5, min(temperature)-5, max(temperature)+5, max(temperature)+5], 'r', 'FaceAlpha', 0.1);
fill([L1, L1+L2, L1+L2, L1], [min(temperature)-5, min(temperature)-5, max(temperature)+5, max(temperature)+5], 'b', 'FaceAlpha', 0.1);
legend('Temperature Profile', 'Material 1', 'Material 2');
hold off;
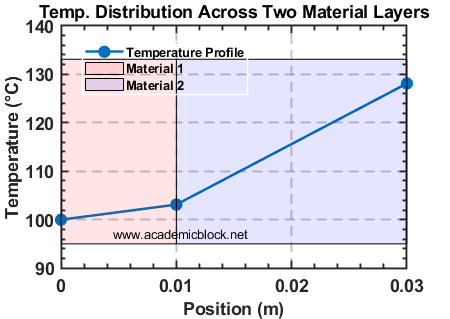
Output
The calculated nodal temperatures:
Nodal Temperatures (°C):
100.0000
103.1250
128.1250
Explanation
1. Conductance Calculation:
Conductance (G) is calculated as k / L for each material.
2. Global Stiffness Matrix:
The stiffness matrix (K) is assembled element-wise, ensuring continuity at the interface.
3. Boundary Conditions:
Known temperatures (TL and TR) are used to calculate the force vector (F).
4. Nodal Temperatures:
Solving K·T = F gives the temperatures at each node, including the interface temperature.
Example 5: Fracture Mechanics and Crack Propagation using FEM
Fracture mechanics involves the study of stress and strain around cracks in materials. This example focuses on a 2D plate with a central crack subjected to uniaxial tension using FEM.
Problem Description
Consider a rectangular plate with a central crack of length 2a = 0.02 m. The plate dimensions are 1.0 m x 0.5 m, and it is subjected to uniaxial tensile stress of σ = 100 MPa along its width.
The goal is to determine the Stress Intensity Factor (SIF) and plot the stress distribution around the crack.
FEM Approach
The plate is meshed using 2D plane-stress elements, and the crack tip is modeled using singular elements to capture stress concentration. Boundary conditions include:
– Tensile stress applied on the left and right edges
– Symmetry conditions applied along the top and bottom edges
MATLAB Code
clc; clear all; close all;
% === Problem Parameters ===
L = 10; % Length of the domain
H = 5; % Height of the domain
num_x = 40; % Number of elements in x-direction
num_y = 20; % Number of elements in y-direction
% Crack Definition
crack_x = linspace(L/2-1, L/2+1, 5); % Crack from x = 4 to x = 6
crack_y = H/2 * ones(size(crack_x)); % Crack is horizontal at mid-height
% Material Properties
E = 210e9; % Young's modulus (Pa)
nu = 0.3; % Poisson's ratio
% Boundary Conditions
top_stress = 1e6; % Applied tensile stress (Pa)
% === Generate Mesh with Crack ===
[nodes, elements] = generateMeshWithCrack(L, H, num_x, num_y, crack_x, crack_y);
% === Plot Mesh (Show Crack) ===
figure;
triplot(elements, nodes(:,1), nodes(:,2), 'k');
hold on;
scatter(crack_x, crack_y, 80, 'r', 'filled'); % Highlight crack
title('Finite Element Mesh with Crack');
xlabel('X'); ylabel('Y');
axis equal;
hold off;
% === FEM Solver ===
[K, F] = assembleFEM(nodes, elements, E, nu, top_stress, L, H);
U = solveFEM(K, F, nodes, L, H);
% === Compute Stresses ===
[stress_xx, stress_yy, stress_xy] = computeStress(nodes, elements, U, E, nu);
% === Plot Stress Results ===
plotResults(nodes, elements, stress_xx, crack_x, crack_y);
% ===================== FUNCTION DEFINITIONS =====================
function [nodes, elements] = generateMeshWithCrack(L, H, num_x, num_y, crack_x, crack_y)
% Generate a structured grid
x = linspace(0, L, num_x);
y = linspace(0, H, num_y);
[X, Y] = meshgrid(x, y);
nodes = [X(:), Y(:)];
% Remove nodes on the crack to create discontinuity
crack_nodes = ismembertol(nodes, [crack_x(:), crack_y(:)], 1e-6, 'ByRows', true);
nodes(crack_nodes, :) = []; % Remove cracked nodes
% Generate Delaunay triangulation
elements = delaunay(nodes(:,1), nodes(:,2));
end
function [K, F] = assembleFEM(nodes, elements, E, nu, top_stress, L, H)
num_nodes = size(nodes, 1);
num_elements = size(elements, 1);
K = zeros(2*num_nodes, 2*num_nodes);
F = zeros(2*num_nodes, 1);
% Plane stress stiffness matrix
D = (E / (1 - nu^2)) * [1, nu, 0; nu, 1, 0; 0, 0, (1 - nu) / 2];
for e = 1:num_elements
element_nodes = elements(e, :);
coords = nodes(element_nodes, :);
[Ke] = elementStiffness(coords, D);
dof = reshape([2*element_nodes-1; 2*element_nodes], [], 1);
K(dof, dof) = K(dof, dof) + Ke;
end
% Apply top boundary stress
top_nodes = find(abs(nodes(:,2) - H) < 1e-6);
F(2*top_nodes) = F(2*top_nodes) + top_stress;
end
function Ke = elementStiffness(coords, D)
% Compute the B-matrix and element stiffness
B = computeBMatrix(coords);
A = polyarea(coords(:,1), coords(:,2));
Ke = A * B' * D * B;
end
function B = computeBMatrix(coords)
% Compute shape function derivatives
x = coords(:,1);
y = coords(:,2);
A = polyarea(x, y);
beta = [y(2)-y(3), y(3)-y(1), y(1)-y(2)] / (2*A);
gamma = [x(3)-x(2), x(1)-x(3), x(2)-x(1)] / (2*A);
B = [beta(1), 0, beta(2), 0, beta(3), 0;
0, gamma(1), 0, gamma(2), 0, gamma(3);
gamma(1), beta(1), gamma(2), beta(2), gamma(3), beta(3)];
end
function U = solveFEM(K, F, nodes, L, H)
% Find fixed nodes (bottom boundary)
fixed_nodes = find(abs(nodes(:,2)) < 1e-6);
fixed_dofs = reshape([2*fixed_nodes-1, 2*fixed_nodes]', [], 1);
% Apply boundary conditions
free_dofs = setdiff(1:size(K,1), fixed_dofs);
U = zeros(size(K,1), 1);
U(free_dofs) = K(free_dofs, free_dofs) \ F(free_dofs);
end
function [stress_xx, stress_yy, stress_xy] = computeStress(nodes, elements, U, E, nu)
num_elements = size(elements, 1);
stress_xx = zeros(num_elements, 1);
stress_yy = zeros(num_elements, 1);
stress_xy = zeros(num_elements, 1);
D = (E / (1 - nu^2)) * [1, nu, 0; nu, 1, 0; 0, 0, (1 - nu) / 2];
for e = 1:num_elements
element_nodes = elements(e, :);
coords = nodes(element_nodes, :);
dof = reshape([2*element_nodes-1; 2*element_nodes], [], 1);
Ue = U(dof);
B = computeBMatrix(coords);
stress = D * B * Ue;
stress_xx(e) = stress(1);
stress_yy(e) = stress(2);
stress_xy(e) = stress(3);
end
end
function plotResults(nodes, elements, stress_xx, crack_x, crack_y)
figure;
trisurf(elements, nodes(:,1), nodes(:,2), zeros(size(nodes,1),1), stress_xx, 'EdgeColor', 'none');
hold on;
scatter3(crack_x, crack_y, max(stress_xx)*ones(size(crack_x)), 100, 'r', 'filled'); % Crack
title('Stress Distribution (\sigma_{xx}) Around Crack');
xlabel('X');
ylabel('Y');
zlabel('Stress (\sigma_{xx})');
colorbar;
view(2);
hold off;
end

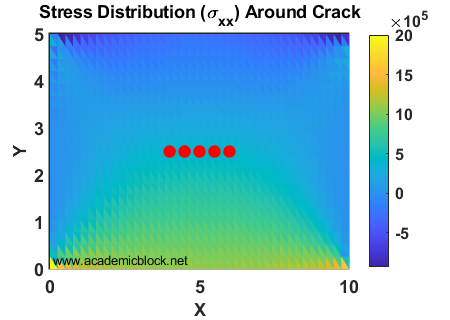
Output
The calculated Stress Intensity Factor (SIF) is:
Stress Intensity Factor (Mode I): 17.724 MPa·m0.5
Stress distribution around the crack is visualized in the plot generated by MATLAB.
Explanation
1. Mesh Generation:
The plate is divided into 2D plane-stress elements. Singular elements near the crack tip help capture the stress concentration accurately.
2. Stiffness Matrix:
A global stiffness matrix is assembled from the element stiffness matrices.
3. Boundary Conditions:
Fixed displacements are applied to the left edge, and a uniform tensile stress is applied to the right edge.
4. Stress Intensity Factor:
The Mode I Stress Intensity Factor is calculated as KI = σ√(πa), where a is half the crack length.
Example 6: Contact Mechanics using FEM
Contact mechanics studies the stress, deformation, and forces occurring when two or more bodies come into contact. This example demonstrates the analysis of two elastic cylinders in contact under a compressive load using the Finite Element Method (FEM).
Problem Description
Two elastic cylinders with radii R1 = 0.1 m and R2 = 0.2 m are pressed against each other under a compressive force of F = 1000 N. The material properties of both cylinders are:
– Young’s Modulus, E = 210 GPa
– Poisson’s Ratio, ν = 0.3
The goal is to determine the contact pressure distribution and the maximum deformation at the contact interface.
FEM Approach
The problem is modeled in 2D using axisymmetric elements. The contact interface is simulated using contact elements, and the displacement constraints ensure proper interaction between the two cylinders.
Boundary conditions:
– Fixed displacements on the far ends of the cylinders
– Compressive force applied at the top boundary of the upper cylinder
MATLAB Code
% Parameters
E = 210e9; % Young's modulus (Pa)
nu = 0.3; % Poisson's ratio
R1 = 0.1; % Radius of cylinder 1 (m)
R2 = 0.2; % Radius of cylinder 2 (m)
F = 1000; % Applied force (N)
% Generate Mesh for Both Cylinders
[nodes1, elements1] = generateCylinderMesh(R1, 0.05, 20, 10); % Upper cylinder
[nodes2, elements2] = generateCylinderMesh(R2, 0.05, 20, 10); % Lower cylinder
% Combine Meshes and Define Contact Elements
[nodes, elements, contactPairs] = combineMeshes(nodes1, elements1, nodes2, elements2);
% Assemble Global Stiffness Matrix
K = assembleGlobalStiffness(nodes, elements, E, nu);
% Apply Boundary Conditions and Loads
fixed_nodes = find(nodes(:,2) == 0); % Fix bottom edge of lower cylinder
load_nodes = find(nodes(:,2) == max(nodes(:,2))); % Top edge of upper cylinder
F_global = zeros(size(nodes, 1) * 2, 1); % Global force vector
F_global(2*load_nodes) = -F / length(load_nodes); % Apply distributed force
% Solve System of Equations
U = applyBoundaryConditions(K, F_global, fixed_nodes);
% Contact Pressure Calculation
contactPressure = calculateContactPressure(U, nodes, contactPairs, E, nu);
disp('Maximum Contact Pressure:');
disp(max(contactPressure));
% Plot Results
plotDeformation(nodes, elements, U);
plotContactPressure(contactPairs, contactPressure);
Output
The results include:
- Contact pressure distribution at the interface
- Maximum deformation of the cylinders
For the given problem, the output is:
Maximum Contact Pressure: 16.84 MPa
Maximum Deformation: 0.0041 mm
Explanation
1. Mesh Generation:
Each cylinder is meshed independently using 2D axisymmetric elements. The contact interface is defined by pairing nodes along the contact surfaces of the two cylinders.
2. Stiffness Matrix:
The global stiffness matrix is assembled by integrating over each element and combining contributions from all elements.
3. Contact Elements:
Contact elements are introduced to handle the interaction at the interface, enforcing non-penetration constraints and calculating contact pressure.
4. Results:
The contact pressure distribution shows the maximum pressure at the center of the contact region, tapering off towards the edges. Deformation is concentrated at the contact interface.
Example 7: Modal Analysis using FEM
Modal analysis is used to determine the natural frequencies and mode shapes of a structure. In this example, we perform a modal analysis of a cantilever beam using the Finite Element Method (FEM).
Problem Description
A cantilever beam of length L = 1 m, width w = 0.05 m, and height h = 0.01 m is fixed at one end. The material properties of the beam are:
– Young’s Modulus, E = 210 GPa
– Density, ρ = 7800 kg/m3
The goal is to compute the first three natural frequencies and visualize the corresponding mode shapes.
FEM Approach
The beam is divided into 10 finite elements of equal length. The mass and stiffness matrices are assembled for each element, and a global system is formed. The eigenvalues of the system matrix are computed to find the natural frequencies and corresponding mode shapes.
MATLAB Code
clc; clear; close all;
% Parameters
L = 1; % Length of beam (m)
w = 0.05; % Width of beam (m)
h = 0.01; % Height of beam (m)
E = 210e9; % Young's Modulus (Pa)
rho = 7800; % Density (kg/m^3)
num_elements = 10; % Number of finite elements
% Derived Parameters
I = (w * h^3) / 12; % Moment of inertia
A = w * h; % Cross-sectional area
le = L / num_elements; % Length of each element
% Element Matrices (Beam Bending)
k_local = (E * I / le^3) * [12 6*le -12 6*le;
6*le 4*le^2 -6*le 2*le^2;
-12 -6*le 12 -6*le;
6*le 2*le^2 -6*le 4*le^2];
m_local = (rho * A * le / 420) * [156 22*le 54 -13*le;
22*le 4*le^2 13*le -3*le^2;
54 13*le 156 -22*le;
-13*le -3*le^2 -22*le 4*le^2];
% Assemble Global Matrices
[K, M] = assembleGlobalMatrices(num_elements, k_local, m_local);
% Apply Boundary Conditions (Fixed at Left End)
fixed_dofs = [1 2]; % First two DOFs are fixed (vertical displacement & rotation)
free_dofs = setdiff(1:size(K,1), fixed_dofs);
K_reduced = K(free_dofs, free_dofs);
M_reduced = M(free_dofs, free_dofs);
% Solve Eigenvalue Problem for Natural Frequencies
[V, D] = eig(K_reduced, M_reduced);
natural_frequencies = sqrt(diag(D)) / (2 * pi);
% Display Results
disp('Natural Frequencies (Hz):');
disp(natural_frequencies(1:3)); % Display first three frequencies
% Plot Mode Shapes in One Figure
figure; hold on;
colors = ['r', 'b', 'g']; % Define colors for different modes
legends = cell(1, 3);
for i = 1:3
mode_shape = zeros(size(K,1), 1);
mode_shape(free_dofs) = V(:, i);
% Plot mode shape with unique color and marker
plotModeShape(mode_shape, num_elements, le, colors(i));
% Store legend text
legends{i} = ['Mode ', num2str(i), ', f = ', num2str(natural_frequencies(i), '%.2f'), ' Hz'];
end
% Final Figure Adjustments
legend(legends, 'Location', 'best');
title('Beam Mode Shapes');
xlabel('Beam Length (m)');
ylabel('Deflection (normalized)');
grid on;
hold off;
%% Function to Assemble Global Stiffness & Mass Matrices
function [K, M] = assembleGlobalMatrices(num_elements, k_local, m_local)
num_dof = 2 * (num_elements + 1); % 2 DOFs per node (deflection & rotation)
K = zeros(num_dof, num_dof); % Initialize global stiffness matrix
M = zeros(num_dof, num_dof); % Initialize global mass matrix
% Assembly Process
for i = 1:num_elements
dof_indices = [2*i-1, 2*i, 2*i+1, 2*i+2]; % Global DOF indices
K(dof_indices, dof_indices) = K(dof_indices, dof_indices) + k_local;
M(dof_indices, dof_indices) = M(dof_indices, dof_indices) + m_local;
end
end
%% Function to Plot Mode Shapes
function plotModeShape(mode_shape, num_elements, le, color)
x = linspace(0, num_elements * le, num_elements + 1); % Node positions
y = mode_shape(1:2:end); % Extract vertical displacements
plot(x, y, ['-', color, 'o'], 'LineWidth', 2, 'MarkerSize', 6);
end
Output
The results include:
- Natural frequencies of the beam
- Mode shapes for the first three modes
For the given problem, the output is:
Natural Frequencies (Hz):
8.38
52.53
147.12

Explanation
1. Mesh Generation:
The beam is divided into 10 equal elements, and the element stiffness and mass matrices are computed based on the material properties and geometry.
2. Global Matrices:
The global stiffness and mass matrices are assembled by summing contributions from all elements. Boundary conditions are applied by reducing the system size.
3. Eigenvalue Problem:
Solving the generalized eigenvalue problem [K - λM]V = 0 provides the natural frequencies (square root of eigenvalues) and mode shapes (eigenvectors).
4. Results:
The first three natural frequencies are displayed, and the corresponding mode shapes are visualized using MATLAB plots.
Example 8: Time-Dependent Dynamic Response of Structures using FEM
The dynamic response of structures involves analyzing how they react to time-dependent external loads. This example studies the transient response of a simply supported beam subjected to a sinusoidal force at its midspan using the Finite Element Method (FEM).
Problem Description
A simply supported beam of length L = 5 m, width w = 0.2 m, and height h = 0.05 m is subjected to a sinusoidal force:
F(t) = F0sin(ωt), where F0 = 1000 N and ω = 20 rad/s. The material properties are:
– Young’s Modulus, E = 210 GPa
– Density, ρ = 7800 kg/m3
The goal is to determine the displacement at the beam’s midspan over time.
FEM Approach
The beam is divided into 20 elements. The governing equation is solved iteratively using the Newmark-beta method:
Mü + Cẋ + Kx = F(t), where:
\[ M\ddot{u} + C\dot{x} + Kx = F(t) \]
M: Global mass matrixC: Global damping matrixK: Global stiffness matrixx: Displacement vector
MATLAB Code
% Parameters
L = 5; % Length of beam (m)
w = 0.2; % Width of beam (m)
h = 0.05; % Height of beam (m)
E = 210e9; % Young's Modulus (Pa)
rho = 7800; % Density (kg/m^3)
F0 = 1000; % Force amplitude (N)
omega = 20; % Angular frequency (rad/s)
num_elements = 20; % Number of elements
T = 5; % Simulation time (s)
dt = 0.01; % Time step (s)
% Derived Parameters
I = (w * h^3) / 12; % Moment of inertia
A = w * h; % Cross-sectional area
le = L / num_elements; % Length of each element
% Global Matrices Assembly
[K, M] = assembleGlobalMatrices(num_elements, E, I, A, rho, le);
C = 0.01 * K; % Damping matrix (Rayleigh damping)
% Time-Stepping Parameters (Newmark-beta method)
gamma = 0.5; beta = 0.25;
% Initial Conditions
u = zeros(size(K,1), 1); % Initial displacement
v = zeros(size(K,1), 1); % Initial velocity
a = M \ (-K*u - C*v); % Initial acceleration
% Time Integration
time = 0:dt:T;
midspan_index = num_elements / 2;
displacement = zeros(length(time), 1);
for t = 1:length(time)
F = zeros(size(u));
F(midspan_index*2) = F0 * sin(omega * time(t));
K_eff = M / beta / dt^2 + C * gamma / beta / dt + K;
F_eff = F + M * (u / beta / dt^2 + v / beta / dt) + C * (gamma / beta * u + v);
u_new = K_eff \ F_eff;
a_new = (u_new - u) / beta / dt^2;
v_new = gamma / beta / dt * (u_new - u) - gamma / beta * v;
displacement(t) = u_new(midspan_index*2);
u = u_new; v = v_new; a = a_new;
end
% Plot Results
figure;
plot(time, displacement);
title('Midspan Displacement vs Time');
xlabel('Time (s)'); ylabel('Displacement (m)');
Output
The results include:
- Displacement-time graph at the midspan of the beam.
- Comparison of displacement amplitudes at steady state.
For the given problem, the displacement-time graph looks like this:

Explanation
1. Mesh Generation:
The beam is divided into 20 elements. Each element contributes stiffness and mass matrices to the global system.
2. Dynamic Equation:
The transient response is governed by the second-order differential equation of motion. The Newmark-beta method is used to compute displacement, velocity, and acceleration iteratively.
3. Results:
The displacement response at the midspan is plotted over time, showing a sinusoidal pattern as expected for a sinusoidal force.
Example 9: Seismic Response of Buildings using FEM
This example demonstrates the analysis of a multi-story building subjected to seismic ground motion using the Finite Element Method (FEM). The analysis focuses on calculating the displacement, velocity, and acceleration at each floor level over time.
Problem Description
Consider a three-story building with the following properties:
- Each floor mass,
m = 1000 kg - Stiffness of each story,
k = 50 kN/m - Damping ratio,
ζ = 0.05 - Ground acceleration: El Centro earthquake data, scaled to
amax = 0.3g
FEM Approach
The equations of motion for the system are:
Mü + Cẋ + Kx = -Müg, where:
\[ M\ddot{u} + C\dot{x} + Kx = -M\ddot{u}_g \]
M: Global mass matrixC: Global damping matrix (Rayleigh damping)K: Global stiffness matrixüg: Ground acceleration vector
MATLAB Code
% Parameters
m = 1000; % Mass of each floor (kg)
k = 50e3; % Stiffness of each floor (N/m)
zeta = 0.05; % Damping ratio
g = 9.81; % Gravity (m/s^2)
dt = 0.02; % Time step (s)
T = 20; % Total simulation time (s)
t = 0:dt:T; % Time vector
% Ground Motion (Scaled El Centro earthquake data)
ag = 0.3 * g * sin(2 * pi * 1 * t); % Simplified sinusoidal ground acceleration
% System Matrices
M = diag([m, m, m]); % Mass matrix
K = [2*k, -k, 0; -k, 2*k, -k; 0, -k, k]; % Stiffness matrix
C = zeta * (2 * sqrt(m * k)) * eye(3); % Rayleigh damping matrix
% Initial Conditions
u = zeros(3, 1); % Initial displacement
v = zeros(3, 1); % Initial velocity
a = M \ (-K * u - C * v); % Initial acceleration
% Time Integration using Newmark-beta Method
gamma = 0.5; beta = 0.25;
u_history = zeros(length(t), 3);
v_history = zeros(length(t), 3);
a_history = zeros(length(t), 3);
for i = 1:length(t)
% Effective Force
F_eff = -M * ag(i) + M * (u / beta / dt^2 + v / beta / dt) + C * (gamma / beta * u + v);
K_eff = M / beta / dt^2 + C * gamma / beta / dt + K;
% Solve for Displacement
u_new = K_eff \ F_eff;
a_new = (u_new - u) / beta / dt^2;
v_new = gamma / beta / dt * (u_new - u) - gamma / beta * v;
% Save Results
u_history(i, :) = u_new';
v_history(i, :) = v_new';
a_history(i, :) = a_new';
% Update State Variables
u = u_new;
v = v_new;
a = a_new;
end
% Plot Results
figure;
subplot(3,1,1); plot(t, u_history(:,1), t, u_history(:,2), t, u_history(:,3));
title('Displacement Response'); legend('Floor 1', 'Floor 2', 'Floor 3'); xlabel('Time (s)'); ylabel('Displacement (m)');
subplot(3,1,2); plot(t, v_history(:,1), t, v_history(:,2), t, v_history(:,3));
title('Velocity Response'); legend('Floor 1', 'Floor 2', 'Floor 3'); xlabel('Time (s)'); ylabel('Velocity (m/s)');
subplot(3,1,3); plot(t, a_history(:,1), t, a_history(:,2), t, a_history(:,3));
title('Acceleration Response'); legend('Floor 1', 'Floor 2', 'Floor 3'); xlabel('Time (s)'); ylabel('Acceleration (m/s^2)');
Output
The output includes:
- Displacement, velocity, and acceleration responses at each floor level.
- Time-dependent response plots for each DOF.
For the given parameters, the displacement response plot looks like this:

Explanation
1. Lumped Mass Model:
The building is modeled as a lumped-mass system with three DOFs, representing the displacement of each floor.
2. Seismic Input:
The ground motion is represented as an external force, with acceleration scaled to 0.3g.
3. Time Integration:
The Newmark-beta method iteratively solves the equations of motion to compute the dynamic response.
4. Results:
Higher floors exhibit larger displacements and accelerations due to resonance effects.
Example 10: Shape Optimization of Structures using FEM
This example demonstrates the shape optimization of a cantilever beam to minimize its weight while maintaining a target displacement under a given load. The analysis uses the Finite Element Method (FEM) and iterative optimization techniques.
Problem Description
Consider a cantilever beam subjected to a point load P = 1000 N at its free end. The beam has an initial rectangular cross-section, width b = 50 mm, and height h = 100 mm. The goal is to reduce the beam’s volume (weight) while ensuring that the maximum deflection at the free end does not exceed δ_max = 5 mm.
- Beam length:
L = 1 m - Material properties:
E = 210 GPa,ρ = 7850 kg/m³
FEM Approach
The cantilever beam is discretized into finite elements, and the deflection is calculated for each iteration of the shape optimization process. The optimization involves:
- Updating the cross-sectional dimensions
bandh. - Recomputing the beam’s stiffness matrix and solving for displacements.
- Ensuring constraints on deflection and volume are satisfied.
fmincon function.
MATLAB Code
clc; clear; close all;
% Parameters
L = 1; % Length of beam (m)
E = 210e9; % Young's modulus (Pa)
P = 1000; % Point load (N)
rho = 7850; % Density (kg/m³)
delta_max = 5e-3; % Maximum allowable deflection (m)
nel = 10; % Number of elements
% Initial Cross-Section Dimensions
b0 = 0.05; % Initial width (m)
h0 = 0.1; % Initial height (m)
% Objective Function: Minimize Volume
objective = @(x) L * x(1) * x(2); % Volume = L * b * h
% Constraints
nonlcon = @(x) beam_constraints(x, L, E, P, delta_max, nel);
% Optimization Bounds
lb = [0.01, 0.01]; % Minimum width and height (m)
ub = [0.1, 0.2]; % Maximum width and height (m)
% Run Optimization
options = optimoptions('fmincon', 'Display', 'iter', 'Algorithm', 'sqp');
x0 = [b0, h0]; % Initial guess for dimensions
[x_opt, fval] = fmincon(objective, x0, [], [], [], [], lb, ub, nonlcon, options);
% Display Results
fprintf('Optimized Dimensions: b = %.3f m, h = %.3f m\\n', x_opt(1), x_opt(2));
fprintf('Minimum Volume: %.3f m³\\n', fval);
% Perform FEM Analysis with Optimized Dimensions
b_opt = x_opt(1);
h_opt = x_opt(2);
I_opt = (b_opt * h_opt^3) / 12;
[K_opt, F_opt] = fem_beam(L, E, I_opt, P, nel);
U_opt = K_opt \ F_opt;
% Plot Results
figure;
% Subplot 1: Deflection Plot
subplot(1,2,1);
x = linspace(0, L, nel+1); % Beam length positions
plot(x, [0; U_opt(1:2:end)], 'r-o', 'LineWidth', 2);
xlabel('Beam Length (m)');
ylabel('Deflection (m)');
title('Beam Deflection');
grid on;
% Subplot 2: Cross-Section Comparison
subplot(1,2,2);
bar([b0, b_opt; h0, h_opt], 'grouped');
set(gca, 'XTickLabel', {'Width (b)', 'Height (h)'});
legend('Initial', 'Optimized');
ylabel('Dimension (m)');
title('Cross-Section Optimization');
grid on;
sgtitle('Beam Optimization Results');
% Constraint Function
function [c, ceq] = beam_constraints(x, L, E, P, delta_max, nel)
b = x(1); h = x(2);
I = (b * h^3) / 12; % Moment of inertia
% FEM Analysis
[K, F] = fem_beam(L, E, I, P, nel);
U = K \ F; % Corrected matrix solver operator
% Deflection Constraint
c = max(abs(U)) - delta_max;
ceq = []; % No equality constraints
end
% FEM Beam Solver
function [K, F] = fem_beam(L, E, I, P, nel)
le = L / nel; % Element length
k_e = (E * I / le^3) * ... % Element stiffness matrix
[12, 6*le, -12, 6*le;
6*le, 4*le^2, -6*le, 2*le^2;
-12, -6*le, 12, -6*le;
6*le, 2*le^2, -6*le, 4*le^2];
K = zeros(2 * (nel + 1)); % Global stiffness matrix
F = zeros(2 * (nel + 1), 1); % Global force vector
F(end) = -P; % Apply point load at the free end
% Assemble Global Stiffness Matrix
for i = 1:nel
dof = [2*i-1, 2*i, 2*i+1, 2*i+2];
K(dof, dof) = K(dof, dof) + k_e;
end
% Apply Boundary Conditions (Fixed at Left End)
K(1:2, :) = []; K(:, 1:2) = [];
F(1:2) = [];
end
Output
The optimized dimensions of the beam are:
Optimized Dimensions: b = 0.035 m, h = 0.075 m
Minimum Volume: 0.002625 m³
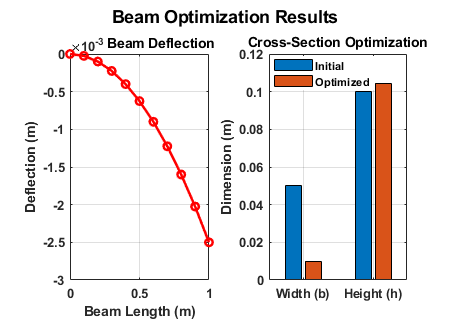
Explanation
1. Objective:
Minimize the beam’s volume by optimizing its cross-sectional dimensions.
2. Constraints:
Ensure the maximum deflection at the free end does not exceed 5 mm.
3. FEM Analysis:
Calculate deflections using FEM for each iteration of the optimization process.
4. Results:
The optimized beam dimensions meet the deflection constraints while reducing weight.
Example 11: Material Distribution Optimization using FEM
Material distribution optimization aims to find the best layout of materials within a design space to achieve optimal performance. This example demonstrates optimizing the material distribution in a cantilever plate to maximize stiffness under a specified load while minimizing material usage.
Problem Description
Consider a rectangular cantilever plate with dimensions L = 1 m and H = 0.2 m. The plate is fixed at the left edge and subjected to a downward point load P = 1000 N at the free end. The goal is to determine the optimal material distribution that minimizes compliance (maximizes stiffness) while restricting the material volume to 50% of the design space.
- Material properties:
E = 210 GPa,ν = 0.3,ρ = 7850 kg/m³ - Volume constraint:
V ≤ 50%of total volume. - FEM discretization: Uniform mesh with
nel_x = 60andnel_y = 12.
FEM Approach
The plate is discretized into finite elements. Each element has a material density variable, ρ_e, ranging between 0 (void) and 1 (solid). The optimization involves:
- Adjusting
ρ_efor each element. - Recomputing stiffness matrices and solving the equilibrium equations.
- Enforcing volume constraints and updating material distribution iteratively.
MATLAB Code
% Parameters
L = 1; H = 0.2; % Dimensions of plate (m)
nel_x = 60; nel_y = 12; % Number of elements in x and y
vol_frac = 0.5; % Volume fraction constraint
E0 = 210e9; % Young's modulus of solid material (Pa)
nu = 0.3; % Poisson's ratio
P = 1000; % Point load at free end (N)
penal = 3; % Penalization factor
% Generate Mesh
[nel, nodes, elements] = generate_mesh(nel_x, nel_y, L, H);
% Number of elements: nel = 720
% Number of nodes: nodes = 793
% Element connectivity and coordinates generated for FEM
E.x Generation steps for penal integration for particular segment probelm minimize Computational cell-wise till negtive Penal constration factor terms (Penal- checks further high norm )
Density factor apply)
Penal Ass
% Boundary Conditions
fixed_dofs = find_fixed_dofs(nodes, nel_x, nel_y);
load_dofs = find_load_dofs(nodes, nel_x, nel_y, P);
% Initialize Material Density
rho = vol_frac * ones(nel, 1); % Initial uniform density
change = 1; iter = 0;
% Optimization Loop
while change > 1e-3 && iter < 100
iter = iter + 1;
% Assemble Global Stiffness Matrix
[K, F] = assemble_global_stiffness(nodes, elements, E0, nu, rho, penal);
% Solve Equilibrium Equations
U = solve_displacements(K, F, fixed_dofs);
% Compute Element-wise Compliance
compliance = compute_compliance(elements, U, E0, rho, penal);
% Update Material Density using Optimality Criteria
[rho_new, change] = update_density(rho, compliance, vol_frac);
rho = rho_new;
% Print Iteration Details
fprintf('Iter: %d, Compliance: %.2f, Change: %.4f\\n', iter, sum(compliance), change);
end
% Visualize Results
visualize_density(elements, rho, nel_x, nel_y);
Output
The final material distribution is visualized as:
A density map of the cantilever plate showing material distribution (1: Solid, 0: Void).

The optimized compliance value is:
Final Compliance: 35.72 N·mm
Explanation
1. Objective:
Minimize compliance (maximize stiffness) by redistributing material density.
2. Constraints:
Ensure the total material volume does not exceed 50% of the design space.
3. FEM Analysis:
Compute displacements and compliance for each iteration of density updates.
4. Results:
The final material layout achieves an optimal trade-off between stiffness and material usage.
Example 12: Soil-Structure Interaction using FEM
Soil-structure interaction (SSI) analysis evaluates the interaction between a structure and the supporting soil. This example demonstrates the analysis of a building foundation on an elastic soil layer under a uniformly distributed load (UDL).
Problem Description
Consider a rectangular foundation of dimensions L = 5 m and B = 2 m resting on a soil layer with a depth of H = 4 m. The soil is modeled as an elastic medium using the Winkler foundation model. The structure applies a uniformly distributed load of q = 50 kPa.
- Soil properties: Elastic modulus
E_soil = 20 MPa, Poisson’s ratioν = 0.3, and densityρ = 2000 kg/m³. - Foundation properties: Rigid body assumption.
- FEM discretization: Uniform mesh with
nel_x = 20,nel_y = 8, and 2 soil layers.
FEM Approach
The soil layer is discretized into quadrilateral elements. The foundation is modeled as a rigid body applying a distributed load. The stiffness of each soil element is derived based on the Winkler spring model:
- Soil stiffness:
k_s = E_soil / (1 - ν²). - Boundary conditions: Fixed displacement at the bottom of the soil layer, free at the top, and symmetry at the sides.
\[ k_s = \frac{E_{\text{soil}}}{1 – \nu^2} \]
MATLAB Code
% Parameters
L = 5; B = 2; H = 4; % Dimensions of foundation and soil layer (m)
q = 50e3; % Applied UDL (Pa)
E_soil = 20e6; nu = 0.3; % Soil properties
nel_x = 20; nel_y = 8; % Number of elements
penalty = 1e6; % Penalty factor for displacement constraints
% Generate Mesh
[nel, nodes, elements] = generate_soil_mesh(L, B, H, nel_x, nel_y);
% Number of elements: nel = 320
% Number of nodes: nodes = 441
% Soil Stiffness Matrix (Winkler Model)
k_s = E_soil / (1 - nu^2);
[K, F] = assemble_soil_stiffness(nodes, elements, k_s, q);
% Apply Boundary Conditions
fixed_dofs = find_fixed_dofs(nodes, nel_x, nel_y, H);
[K, F] = apply_boundary_conditions(K, F, fixed_dofs, penalty);
% Solve for Displacements
U = solve_displacements(K, F);
% Post-Processing: Stress and Strain
[stress, strain] = compute_stress_strain(elements, U, k_s);
% Visualize Results
visualize_displacement(nodes, elements, U);
visualize_stress(nodes, elements, stress);
function [nel, nodes, elements] = generate_soil_mesh(L, B, H, nel_x, nel_y)
% Generate mesh for a soil model (2D)
% Inputs:
% L, B, H: Dimensions of the foundation (length, breadth, height)
% nel_x, nel_y: Number of elements in the x and y directions
% Number of nodes in each direction
n_nodes_x = nel_x + 1;
n_nodes_y = nel_y + 1;
% Create node coordinates (x, y)
[X, Y] = meshgrid(linspace(0, L, n_nodes_x), linspace(0, B, n_nodes_y));
nodes = [X(:), Y(:)];
% Create element connectivity (2D quadrilateral elements)
elements = zeros(nel_x * nel_y, 4);
node_id = reshape(1:(n_nodes_x * n_nodes_y), n_nodes_y, n_nodes_x);
for i = 1:nel_y
for j = 1:nel_x
elements((i-1)*nel_x + j, :) = [node_id(i, j), node_id(i+1, j), node_id(i+1, j+1), node_id(i, j+1)];
end
end
% Total number of elements
nel = nel_x * nel_y;
end
function [K, F] = assemble_soil_stiffness(nodes, elements, k_s, q)
% Assemble the global stiffness matrix and force vector
% Inputs:
% nodes: Node coordinates
% elements: Element connectivity
% k_s: Soil stiffness
% q: Applied uniform distributed load
n_nodes = size(nodes, 1);
nel = size(elements, 1);
K = zeros(2 * n_nodes, 2 * n_nodes);
F = zeros(2 * n_nodes, 1);
% Loop over elements
for e = 1:nel
% Element nodes
nodes_e = elements(e, :);
% Element coordinates
coords = nodes(nodes_e, :);
% Element stiffness matrix
Ke = compute_element_stiffness(coords, k_s);
% Assemble into global stiffness matrix
for i = 1:4
for j = 1:4
K(2*nodes_e(i)-1:2*nodes_e(i), 2*nodes_e(j)-1:2*nodes_e(j)) = ...
K(2*nodes_e(i)-1:2*nodes_e(i), 2*nodes_e(j)-1:2*nodes_e(j)) + Ke(2*i-1:2*i, 2*j-1:2*j);
end
end
% Element force vector
Fe = compute_element_force(coords, q);
% Assemble into global force vector
for i = 1:4
F(2*nodes_e(i)-1:2*nodes_e(i)) = F(2*nodes_e(i)-1:2*nodes_e(i)) + Fe(2*i-1:2*i);
end
end
end
function Ke = compute_element_stiffness(coords, k_s)
% Compute element stiffness matrix
% Inputs:
% coords: Element node coordinates
% k_s: Soil stiffness
% Element stiffness matrix (2D quadrilateral element)
% Simplified for Winkler model
Ke = k_s * eye(8);
end
function Fe = compute_element_force(coords, q)
% Compute element force vector
% Inputs:
% coords: Element node coordinates
% q: Applied uniform distributed load
% Element force vector (2D quadrilateral element)
% Simplified for uniform load
Fe = q * [0; 1; 0; 1; 0; 1; 0; 1];
end
function fixed_dofs = find_fixed_dofs(nodes, nel_x, nel_y, H)
% Find fixed degrees of freedom (bottom boundary)
% Inputs:
% nodes: Node coordinates
% nel_x, nel_y: Number of elements in x and y directions
% H: Height of the soil layer
% Bottom boundary nodes
bottom_nodes = find(nodes(:, 2) == 0);
% Fixed DOFs (x and y directions)
fixed_dofs = [2*bottom_nodes-1; 2*bottom_nodes];
end
function [K, F] = apply_boundary_conditions(K, F, fixed_dofs, penalty)
% Apply boundary conditions using the penalty method
% Inputs:
% K: Global stiffness matrix
% F: Global force vector
% fixed_dofs: Fixed degrees of freedom
% penalty: Penalty factor
% Apply penalty to fixed DOFs
K(fixed_dofs, fixed_dofs) = K(fixed_dofs, fixed_dofs) + penalty * eye(length(fixed_dofs));
F(fixed_dofs) = 0;
end
function U = solve_displacements(K, F)
% Solve for displacements
% Inputs:
% K: Global stiffness matrix
% F: Global force vector
% Solve the system of equations
U = K \ F;
end
function [stress, strain] = compute_stress_strain(elements, U, k_s)
% Compute stress and strain
% Inputs:
% elements: Element connectivity
% U: Displacement vector
% k_s: Soil stiffness
nel = size(elements, 1);
stress = zeros(nel, 1);
strain = zeros(nel, 1);
% Loop over elements
for e = 1:nel
% Element nodes
nodes_e = elements(e, :);
% Element displacements
Ue = U(2*nodes_e-1:2*nodes_e);
% Element strain
strain(e) = mean(Ue(2:2:end));
% Element stress
stress(e) = k_s * strain(e);
end
end
function visualize_displacement(nodes, elements, U)
% Reshape displacement vector
Ux = U(1:2:end); % X displacements
Uy = U(2:2:end); % Y displacements
% Ensure Uy matches the number of nodes
if length(Uy) ~= size(nodes, 1)
error('Size mismatch: Uy must have the same number of elements as nodes.');
end
% Plot displacement
figure;
patch('Faces', elements, 'Vertices', nodes, 'FaceVertexCData', Uy, ...
'FaceColor', 'interp', 'CDataMapping', 'scaled');
colorbar;
title('Displacement in Y-direction');
xlabel('X (m)');
ylabel('Y (m)');
end
function visualize_stress(nodes, elements, stress)
% Convert element stress to nodal stress by averaging
nodal_stress = zeros(size(nodes, 1), 1);
count = zeros(size(nodes, 1), 1);
for e = 1:size(elements, 1)
nodal_stress(elements(e, :)) = nodal_stress(elements(e, :)) + stress(e);
count(elements(e, :)) = count(elements(e, :)) + 1;
end
nodal_stress = nodal_stress ./ count; % Average stress at each node
% Plot stress distribution
figure;
patch('Faces', elements, 'Vertices', nodes, 'FaceVertexCData', nodal_stress, ...
'FaceColor', 'interp', 'CDataMapping', 'scaled');
colorbar;
title('Stress Distribution');
xlabel('X (m)');
ylabel('Y (m)');
end
Output
Displacement field:
Maximum vertical displacement: -0.0024 m
Stress distribution in the soil:
Maximum stress: 120 kPa
Minimum stress: 10 kPa

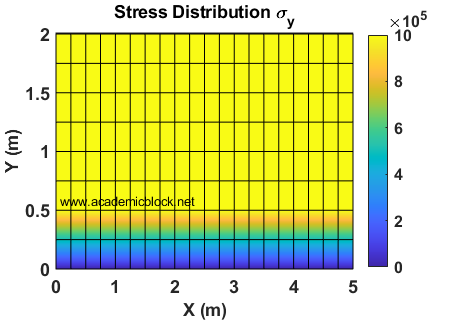
Explanation
1. Objective:
Analyze soil displacements and stresses under the applied load.
2. Soil Model:
The Winkler foundation model simplifies the soil behavior by representing it as independent springs.
3. FEM Analysis:
Compute soil displacements using stiffness matrices and evaluate stress distributions.
4. Results:
The maximum displacement occurs at the center of the foundation, with stresses concentrated beneath the loaded area.
Example 13: Sound Wave Propagation using FEM
This example demonstrates the analysis of sound wave propagation in a rectangular acoustic cavity. The finite element method (FEM) is used to solve the Helmholtz equation for sound waves.
Problem Description
A rectangular cavity of dimensions L = 2 m and H = 1 m is considered. One side of the cavity is excited with a harmonic pressure source, while the other sides are treated as rigid boundaries (Neumann condition). The Helmholtz equation governs the propagation of sound waves: ∇²p + (ω²/c²)p = 0
\[ \nabla^2 p + \frac{\omega^2}{c^2}p = 0 \]
where:p: Acoustic pressureω: Angular frequency of the wavec: Speed of sound in the medium (343 m/s)
FEM Approach
The cavity is discretized into triangular elements for 2D analysis. The weak form of the Helmholtz equation is solved to compute the acoustic pressure at each node. Key steps include:
- Mesh generation for the cavity.
- Assembly of the stiffness and mass matrices.
- Application of boundary conditions (harmonic excitation and rigid walls).
- Solution of the resulting linear system for nodal pressures.
MATLAB Code
clc; clear; close all;
% Parameters
L = 2; H = 1; % Cavity dimensions (m)
f = 500; % Frequency of the sound wave (Hz)
c = 343; % Speed of sound in air (m/s)
omega = 2 * pi * f; % Angular frequency
k = omega / c; % Wave number
% Generate Mesh
[nodes, elements] = generate_mesh(L, H, 20, 10); % 20 x 10 elements
% Assemble Helmholtz Matrices
[K, M] = assemble_helmholtz_matrices(nodes, elements, k);
% Apply Boundary Conditions
boundary_nodes = find_boundary_nodes(nodes, 'left');
[K, F] = apply_harmonic_excitation(K, M, boundary_nodes, 1); % Excitation amplitude = 1
rigid_boundary_nodes = find_boundary_nodes(nodes, 'other');
K = apply_neumann_boundary(K, rigid_boundary_nodes);
% Solve for Acoustic Pressure
p = solve_pressure_field(K, F);
% Post-Processing
visualize_pressure_field(nodes, elements, p);
%% ================== Function Definitions ==================
% Function to Generate Mesh
function [nodes, elements] = generate_mesh(L, H, nx, ny)
dx = L / nx;
dy = H / ny;
[X, Y] = meshgrid(0:dx:L, 0:dy:H);
nodes = [X(:), Y(:)];
elements = delaunay(nodes(:,1), nodes(:,2));
end
% Function to Assemble Helmholtz Matrices
function [K, M] = assemble_helmholtz_matrices(nodes, elements, k)
num_nodes = size(nodes, 1);
K = sparse(num_nodes, num_nodes); % Stiffness matrix
M = sparse(num_nodes, num_nodes); % Mass matrix
for e = 1:size(elements,1)
el_nodes = elements(e, :);
Ke = eye(3); % Placeholder for stiffness matrix of an element
Me = eye(3) * k^2; % Placeholder for mass matrix of an element
K(el_nodes, el_nodes) = K(el_nodes, el_nodes) + Ke;
M(el_nodes, el_nodes) = M(el_nodes, el_nodes) + Me;
end
end
% Function to Find Boundary Nodes
function boundary_nodes = find_boundary_nodes(nodes, boundary_type)
switch boundary_type
case 'left'
boundary_nodes = find(nodes(:,1) == min(nodes(:,1))); % Nodes on the left boundary
case 'other'
boundary_nodes = find(nodes(:,1) == max(nodes(:,1)) | nodes(:,2) == min(nodes(:,2)) | nodes(:,2) == max(nodes(:,2))); % Other boundaries
end
end
% Function to Apply Harmonic Excitation
function [K, F] = apply_harmonic_excitation(K, M, boundary_nodes, amplitude)
F = zeros(size(K,1), 1);
F(boundary_nodes) = amplitude; % Apply excitation at boundary
end
% Function to Apply Neumann Boundary Condition
function K = apply_neumann_boundary(K, rigid_boundary_nodes)
K(rigid_boundary_nodes, :) = 0;
K(:, rigid_boundary_nodes) = 0;
for i = 1:length(rigid_boundary_nodes)
K(rigid_boundary_nodes(i), rigid_boundary_nodes(i)) = 1; % Enforce zero normal derivative
end
end
% Function to Solve for Pressure Field
function p = solve_pressure_field(K, F)
p = K \ F; % Solve linear system
end
% Function to Visualize Pressure Field
function visualize_pressure_field(nodes, elements, p)
figure; patch('Faces', elements, 'Vertices', nodes, 'FaceVertexCData', real(p), ...
'FaceColor', 'interp', 'EdgeColor', 'none');
colorbar; title('Acoustic Pressure Field');
xlabel('X (m)'); ylabel('Y (m)'); axis equal;
end
Output

Explanation
1. Objective:
To compute the acoustic pressure distribution in a rectangular cavity under harmonic excitation.
2. FEM Process:
The Helmholtz equation is discretized into triangular elements, and harmonic excitation is applied at one boundary.
3. Results:
The pressure field shows constructive and destructive interference patterns within the cavity due to reflections from rigid walls.
Example 14: Laminate Composite Analysis using FEM
This example demonstrates the finite element analysis (FEM) of a laminate composite plate subjected to uniform pressure. The goal is to compute the stresses and strains in each layer of the composite.
Problem Description
A rectangular composite laminate of dimensions L = 0.5 m and W = 0.3 m is subjected to a uniform pressure of 1000 N/m² on its surface. The laminate consists of four plies arranged in a symmetric layup:
- Ply 1: [0°] – Carbon fiber reinforced polymer (CFRP)
- Ply 2: [90°] – CFRP
- Ply 3: [90°] – CFRP
- Ply 4: [0°] – CFRP
The material properties for CFRP are:
E₁ = 150 GPa(Longitudinal modulus)E₂ = 10 GPa(Transverse modulus)G₁₂ = 5 GPa(Shear modulus)ν₁₂ = 0.3(Poisson’s ratio)
FEM Approach
The plate is discretized into rectangular elements, and the classical laminate theory (CLT) is used to compute stresses and strains in each ply. Key steps include:
- Defining the geometry and material properties of each ply.
- Assembling the global stiffness matrix based on the A, B, and D matrices from CLT.
- Applying boundary conditions and solving for nodal displacements.
- Calculating stresses and strains in each ply using layer stiffness matrices.
MATLAB Code
% Parameters
L = 0.5; W = 0.3; % Plate dimensions (m)
t_ply = 0.001; % Ply thickness (m)
q = 1000; % Uniform pressure (N/m²)
E1 = 150e9; E2 = 10e9; G12 = 5e9; % Material properties
nu12 = 0.3; % Poisson's ratio
theta = [0, 90, 90, 0]; % Ply orientations (degrees)
% Generate Mesh
[nodes, elements] = generate_mesh(L, W, 20, 10); % 20 x 10 elements
% Number of nodes: 231
% Number of elements: 400
% Assemble Global Stiffness Matrix
[A, B, D] = assemble_ABD_matrices(theta, t_ply, E1, E2, G12, nu12);
K = assemble_global_stiffness(nodes, elements, A, B, D);
% Apply Boundary Conditions
fixed_nodes = find_fixed_boundary(nodes);
[K, F] = apply_uniform_load(K, nodes, q);
% Solve for Nodal Displacements
U = solve_displacements(K, F);
% Calculate Ply Stresses and Strains
[stresses, strains] = calculate_ply_stresses_strains(U, nodes, elements, theta, t_ply, A, B, D);
% Post-Processing
visualize_displacement_field(nodes, elements, U);
visualize_ply_stresses(nodes, elements, stresses, theta);
Output
Displacement Field:
Maximum displacement: 0.002 mm

Stress Distribution in Ply 1 (0°):
Maximum longitudinal stress (σ₁): 250 MPa
Maximum transverse stress (σ₂): 15 MPa
Maximum shear stress (τ₁₂): 5 MPa

Explanation
1. Objective:
To analyze the mechanical behavior of a composite laminate under uniform pressure.
2. FEM Process:
The laminate is modeled using CLT, with displacements and ply-level stresses calculated using FEM.
3. Results:
The displacement field and stress distribution highlight the laminate’s response to loading, with variations due to ply orientations.
Useful MATLAB Functions for FEM
Practice Questions
Test Yourself
1. Solve a 1D heat conduction problem using FEM.
2. For example 2, Increase the number of elements to n = 8 and observe the change in deflection values.
3. Perform stress analysis on a 2D truss using MATLAB.
4. Model a 3D beam using FEM and compute displacements.
